Úvod
Ak v elektrickej sieti vykonáme nejakú zmenu, napr.
pripojíme zdroj, zmeníme hodnotu rezistora, prepínačom zmeníme konfiguráciu
siete a podobne, prúdy a napätia vo vetvách siete sa prispôsobia
týmto zmenám. Ak sieť obsahuje kondenzátory a cievky, ktoré viažu energiu
elektrického, alebo magnetického poľa, toto prispôsobovanie trvá určitý čas.
Javy, ktoré v sieti pri tom prebiehajú, nazývame prechodovými javmi.
V tomto paragrafe ukážeme ako sa správajú napätia a prúdy
v jednoduchej sieti s jednosmerným zdrojom, rezistorom
a kondenzátorom.
Vybíjanie kondenzátora
Vezmime si elektrický obvod, v ktorej je
zdroj jednosmerného napätia U,
vypínač, kondenzátor s kapacitou C a
rezistor s odporom R podľa obr. Obr.
1. V čase t = 0 odpojíme zdroj.
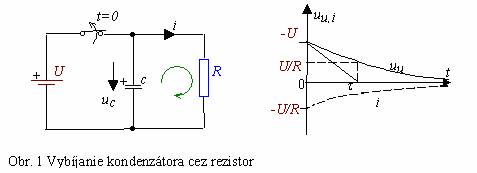
Ostane len do série zapojený kondenzátor s rezistorom
a nastane vybíjanie kondenzátora cez rezistor.
Pre RC
obvod platí 2. Kirchhoffov zákon:
![]() (1)
(1)
kde
prvý člen je napätie na rezistore a druhý člen je
napätie na kondenzátore. Prúd tečie vďaka úbytku náboja q na kondenzátore, t.j. i = -dq/dt , uC = -q/C, čo dosadíme do (1) a
rovnicu upravíme
![]() odkiaľ
odkiaľ ![]()
Integrovaním
dostaneme
![]() odkiaľ
odkiaľ ![]()
Konštantu
k nájdeme z počiatočnej
podmienky q0 = CU v čase t
= 0. Vyjde nám CU = k a posledná rovnica nadobudne tvar
![]() (2)
(2)
Z
náboja môžeme získať napätie na kondenzátore a prúd:
![]()
![]() (3)
(3)
Vidíme,
náboj sa postupne mení od počiatočnej hodnoty q0 = C U postupne k nule. Nemôže sa zmeniť skokom, lebo
na prenos náboja treba vykonať prácu a práca sa nedá vykonať za nulový čas.
Grafy časových závislostí napätia na kondenzátore a prúdu sú na obr. Obr. 1.
Ani napätie na kondenzátore sa nemení skokom. Energia elektrického poľa v
kondenzátore je
We = CU2/2
a ako
vieme, energia sa môže zmeniť len prácou, a teda z rovnakých dôvodov nemôže byť
zmenená skokom.
Nabíjanie kondenzátora
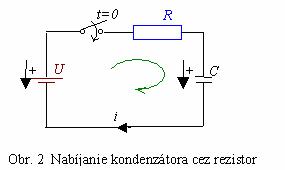
V elektrickom obvode pozostávajúcom zo
zdroja, vypínača, rezistora s odporom R
a kondenzátora s kapacitou C (všetky
prvky sú zapojené sériovo, obr. Obr. 2) v čase t = 0 zapneme vypínač. Obvod bude uzavretou slučkou a môžeme
napísať 2. Kirchhoffov zákon:
![]()
Prúd je
spôsobený prirastaním náboja na kondenzátore, t.j. i = dq/dt a uC = q/C. Po dosadení a úprave
![]() (4)
(4)
Riešenie
homogénnej diferenciálnej rovnice (4) (bez pravej strany) je
![]()
Celkové
riešenie navrhneme také, aby spĺňalo počiatočnú podmienku ![]() .
Riešenie bude
.
Riešenie bude
![]()
Ak do
tejto rovnice dosadíme t =0 ,
dostaneme k = -CU. Takže riešenie
bude
![]() (5)
(5)
Odtiaľto
získame
![]()
![]() (6)
(6)
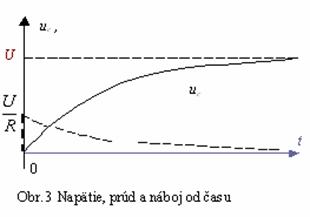
Grafy
závislostí (5), (Obr. 2), (7) sú na obr. Obr. 3.