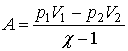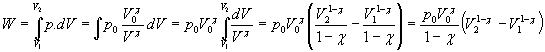I d e á l n y p l y n

Definícia

Pri odvodzovaní zákonov platných pre plyn sa namiesto reálneho plynu zavádza zjednodušený model, ktorý nazývame ideálny plyn.

O molekulách ideálneho plynu vyslovujeme tri predpoklady:

o rozmery molekúl ideálneho plynu sú zanedbateľne malé v porovnaní so strednou vzdialenosťou molekúl

o molekuly ideálneho plynu nepôsobia na seba navzájom príťažlivými silami

o vzájomné zrážky molekúl ideálneho plynu a zrážky týchto molekúl so stenou nádoby sú dokonale pružné

V každom okamihu sa prevažná časť molekúl ideálneho plynu pohybuje voľne rovnomerným priamočiarym pohybom. Keďže molekuly ideálneho plynu nepôsobia na seba navzájom silami, je potenciálna energia sústavy molekúl ideálneho plynu nulová. Vnútorná energia ideálneho plynu sa rovná súčtu kinetických energií jeho molekúl pohybujúcich sa neusporiadaným posuvným pohybom pri normálnych podmienkach (t_n=0 °C, p_n=1,013 25 . 10⁵ Pa) možno väčšinu plynov s dostatočným stupňom presnosti považovať za ideálny plyn.

Návrat

Stavová rovnica

Stavová rovnica je jednou zo základných rovníc termodynamiky a popisuje ako navzájom súvisia jednotlivé stavové veličiny. To je užitočné, lebo nám umožňuje pre danú zmenu jednej zo stavových veličín (napríklad zväčšenie objemu plynu) predpovedať, ako sa budú správať ostatné stavové veličiny. Stavovú rovnicu môžeme napísať pre plyny okolo nás, ale napríklad aj pre vnútro hviezd či celý vesmír.

Najznámejšou je stavová rovnica ideálneho plynu

$,$

kde

$p$ – je tlak plynu [Pa]

$V$ – je jeho objem [m³]

$N$ – je celkový počet jeho častíc

$k$ – je Boltzmannova konštanta (1,38 10^-23 J/K)

$T$ – je teplota plynu [K].

Stavová rovnica sa odvádza pomocou kinetickej teórie plynov. Najdôležitejšie je si uvedomiť, že tlak plynu je daný odrazmi jeho molekúl od stien nádoby a hľadať rýchlosti, ktorými sa tieto molekuly pohybujú (a odrážajú). Celé odvodenie je však pomerne komplikované.

Stavová rovnica ideálneho plynu sa niekedy zapisuje v trochu inom tvare, kedy je počet častíc nahradený ich mólovým množstvom . Rovnica má potom tvar

Konštanta $R$ sa nazýva univerzálna plynová konštanta a má hodnotu približne 8,31 J/mol.K. Jeden mól plynu (n = 1) je také množstvo látky, ktoré obsahuje N_A častíc (molekúl, atómov), N = n N_A = 1 N_A = 6,023.10²³ mol^-1 , kde N_A je Avogadrova konštanta, ktorá predstavuje počet atómov, ktorý sa nachádza v 12 gramoch ¹²C.

Návrat

Práca plynu

Najme valec s pohyblivým piestom o ploche S, v ktorom sa nachádza plyn o tlaku p a objeme V. Plyn pôsobí na piest silou F o veľkosti F = p S kolmou na piest. V prípade posunutia piestu o vzdialenosť dx (pri nezmenenom tlaku), vykoná elementárnu prácu:

Pre elementárnu prácu plynu teda platí: dA = p dV

V prípade posunutia piestu tak, že sa objem plynu zmení z hodnoty V1 na hodnotu V2, vychádza pre prácu vykonanú plynom:

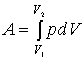
Rovnako veľkú prácu musia vykonať aj vonkajšie sily na to aby sa objem plynu zmenšil z hodnoty V2 na V1. Túto prácu voláme vonkajšia práca a podľa konvenkcie sa berie ako záporná.

Návrat

Prvá veta termodynamická

Prvá veta termodynamická vychádza z predpokladu, že teplo je určitý druh energie a hovorí, že v izolovanej sústave v ktorej dochádza k rôznym premenám energie, je súčet všetkých týchto energií konštantný. Vyjadruje teda zákon zachovania energie. Prvá veta termodynamická má tvar:

kde ΔU - zmena vnútornej energie,

Q - teplo dodané sústave – plynu,

A - práca vykonaná sústavou – plynom.

Vnútorná energia U charakterizuje stav sústavy a voláme ju tiež stavovou funkciou.

Pri používaní 1. vety termodynamickej sa dodržuje nasledovná znamienková konvekcia:

a) teplo Q do sústavy dodané budeme označovať znamienkom + a teplo, ktoré sústava odovzdá znamienkom –

b) nárast vnútornej energie ΔU je vždy kladný a jej úbytok bude záporný

c) za kladnú budeme považovať prácu A, ktorú sústava vykoná/odovzdá do prostredia a prácu, ktorú vykoná vonkajšie prostredie na danej sústave, budeme označovať ako zápornú.

Návrat

Termodynamické deje v ideálnom plyne

Stavová rovnica platí pre každý dej v plyne. Z tejto rovnice môžeme získať rovnice pre špeciálne prípady:

a) Dej pri ktorom je teplota plynu stála T = konšt sa nazýva izotermický dej. Potom

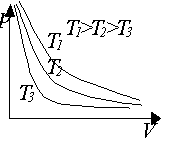
Tieto rovnice sú matematickým vyjadrením Boyle-Mariottovho zákona. Indexy 1, 2 v druhej rovnici zodpovedajú dvom rôznym stavom plynu. graf vyjadrujúci tlak plynu so stálou hmotnosťou ako funkciu jeho objemu pri izotermickom deji sa volá izoterma.

Zmena vnútornej energii plynu pri izotermickom deji sa rovná práci plynu A, ktorú vykoná plyn pri svojej expanzii/kompresii z objemu V₁na objem V₂:

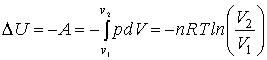
b) Dej pri ktorom je tlak plynu stály p = konšt. sa nazýva izobarický dej pri Potom

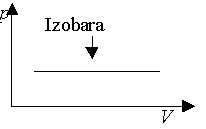
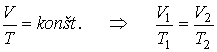
Pri izobarickom deji s ideálnym plynom stálej hmotnosti je objem plynu priamo úmerný jeho termodynamickej teplote (Gay-Lussacov zákon). graf, ktorý vyjadruje tlak plynu so stálou hmotnosťou ako funkciu jeho objemu pri izobarickom deji, volá sa izobara.

Zmena vnútornej energii plynu pri izochorickom deji je rovná teplu Q, ktoré príme plyn počas daného deja:

kde n - je počet mólov plynu a C_V - je merná tepelná kapacita pri konštantnom objeme.

c) izochorický dej pri V = konšt. Potom

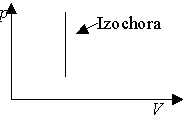
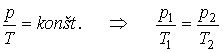
Pri izochorickom deji s ideálnym plynom stálej hmotnosti je tlak plynu priamo úmerný jeho termodynamickej teplote (Charlesov zákon). graf, ktorý vyjadruje tlak plynu so stálou hmotnosťou ako funkciu jeho objemu pri izochorickom deji, volá sa izochora.

Zmena vnútornej energii plynu pri izotermickom deji je rovná teplu Q, ktoré príme plyn počas daného deja a práci plynu A, ktorú vykoná plyn pri svojej expanzii/kompresii z objemu V₁na objem V₂:

kde n - je počet mólov plynu a C_P - je merná tepelná kapacita pri konštantnom tlaku.

d) Pri adiabatickom deji neprebieha tepelná výmena medzi plynom a okolím Q = 0 J, takže podľa prvého termodynamického zákona platí:

Pri adiabatickom stlačení plynu v nádobe sa pôsobením vonkajšej sily koná práca a teplota plynu i jeho vnútorná energia sa zväčšujú. Pri adiabatickom rozpínaní prácu koná plyn a teplota plynu i jeho vnútorná energia zmenšujú

Pre adiabatický dej s ideálnym plynom platí Poissonov zákon:

kde χ je Poissonova konštanta, pričom platí: 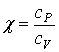. Poissonova konštanta je vždy väčšia ako 1. Závisí od druhu plynu (pre plyn s jednoatómovými molekulami χ = 3/2, s dvojatómovými molekulami χ = 5/2).

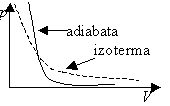Graf, ktorý vyjadruje tlak plynu so stálou hmotnosťou ako funkciu jeho objemu pri adiabatickom deji, volá sa adiabata. Adiabata klesá vždy strmšie ako izoterma toho istého plynu s rovnakou hmotnosťou.

Práca vykonaná pri adiabatickom deji:

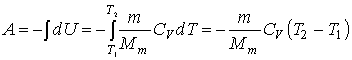
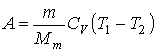
Ďalším z prakticky používaných tvarov pre vyjadrenie práce pri adiabatickom deji dostaneme vylúčením teploty:

Návrat